Calculus formuleblad
Standaardlimieten voor functies
Deprecated: Function ereg() is deprecated in /home/gf4222/domains/ginco.nl/public_html/wb/app/vendors/mathpublisher.php on line 1609
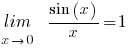
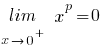 (voor alle p > 0)
(voor alle p > 0)
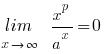 (voor alle p
(voor alle p 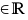 , a > 1)
, a > 1)
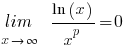 (voor alle p > 0)
(voor alle p > 0)
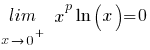 (voor alle p > 0)
(voor alle p > 0)
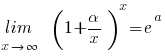 (voor alle
(voor alle 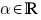 )
)
Standaardlimieten voor rijen
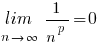 (als p > 0)
(als p > 0)
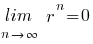 (als
(als 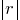 < 1)
< 1)
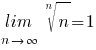
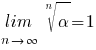 (voor alle
(voor alle 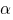 > 0)
> 0)
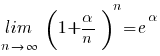 (voor alle
(voor alle 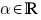 )
)
Afgeleiden van standaardfuncties
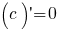
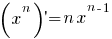
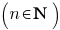
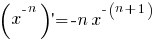
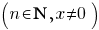
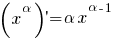
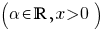
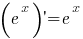
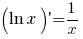 (x > 0)
(x > 0)
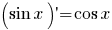
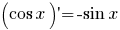
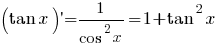
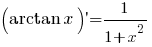
Standaard Taylor ontwikkelingen
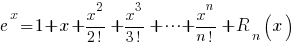
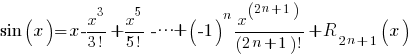
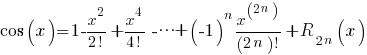
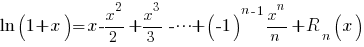
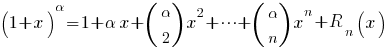
Hierin is 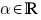 en
en 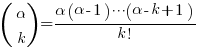 .
.
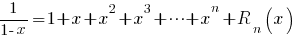
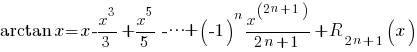
Met restterm 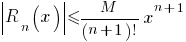 waarbij
waarbij 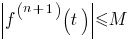 op het interval
op het interval ![delim{[}{0,x}{]} delim{[}{0,x}{]}](/formules/math_986.5_ca9a7907eb4f62cda77b41c1198a948e.png) .
.
Lijst van Primitieven
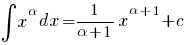 (
(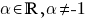 )
)
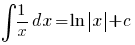 (x > 0 of x < 0)
(x > 0 of x < 0)
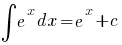
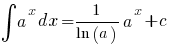 (a > 0, a
(a > 0, a 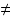 1)
1)
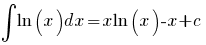 (x > 0)
(x > 0)
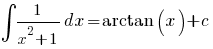
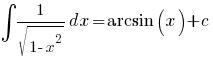 (-1 < x < 1)
(-1 < x < 1)
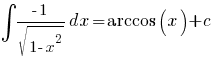 (-1 < x < 1)
(-1 < x < 1)
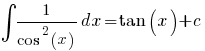 (
(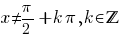 )
)
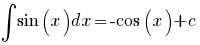
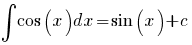
(c) Ginco.nl | Disclaimer